XV Jornadas Luso-Espanholas de Matemática

En este estudio, el profesor Martel presenta una curiosa metodología mediante la construcción de figuras geométricas con triángulos de ángulos 90º, 60º y 30º o triángulos 90º, 45º y 45º, para el análisis de cuestiones geométricas como simetrías, equivalencias, el Teorema de Pitágoras, etc. que son de gran interés en el aula de primaria, porque permiten un aprendizaje activo, basado en la manipulación de materiales.

Para la propuesta manipulativa utiliza escuadras y cartabones, en un uso que no es el conocido en el dibujo lineal y comienza explicando el origen de estos dos instrumentos y el significado de sus términos.

El estudio lo empieza con la construcción de cartabones y escuadras en cartulina, para introducir de forma intuitiva aspectos conceptuales relacionados con los ángulos.

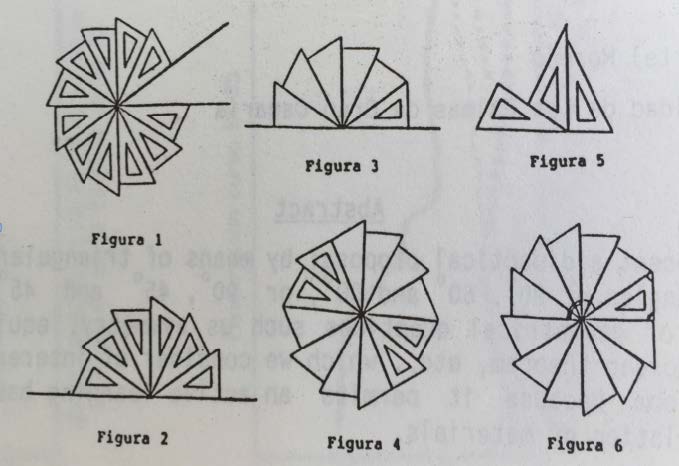
Ángulos y cartabones. Martel, J. (1991)

Posteriormente, realiza una experiencia tomando por una parte, dos cartabones y por otra, dos escuadras; al unir cada pareja por sus lados iguales se obtienen diferentes tipos de bicartabones y diábolos que, según se unan por sus mismas caras o no, permitirían obtener paralelogramos, triángulos, y cometas.

Si en lugar de dos cartabones o dos escuadras, se toman tres, se forman diferentes tipos de trapecios y pentágonos irregulares diversos, hasta componer un total de 8 tricartabones y 4 triábolos; de igual modo, se procede con cuatro cartabones o con cuatro escuadras y se obtiene un buen número de figuras, que analiza en función del número de lados y de sus hipotenusas. Si se continúa uniendo más cartabones y escuadras por separado, de cinco encinco, de seis en seis,…, se observan algunas situaciones curiosas y demostraciones del teorema de Pitágoras, que el autor detalla en el análisis y cuyas ilustraciones se muestran a continuación.

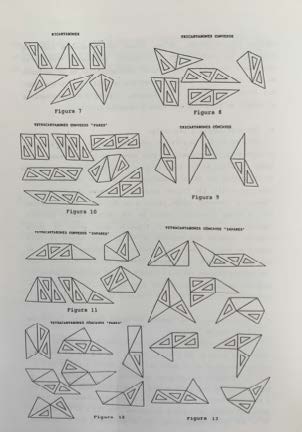
Bicartabones y diábolos, tricartabones y triábolos. Martel, J. (1991)

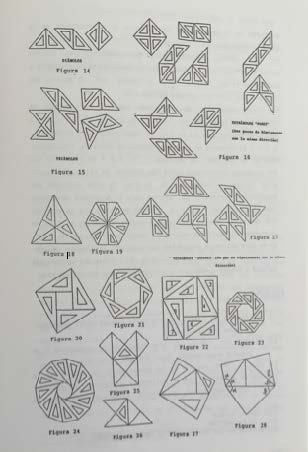
Policartabones y polidiábolos. Martel, J. (1991)

En el estudio siguiente José Martel e hijo, presentan una definición válida, tanto para la física como para las matemáticas, del concepto de Cantidad de una Magnitud; con la intención de eliminar obstáculos para la comprensión por parte del alumno, debido al uso de dos modos distintos para definir un mismo concepto. Muestran aquí también algunos casos o ejemplos dados en textos matemáticos.

Con esta publicación, realizan una propuesta didáctica sobre el uso del concepto de Magnitud, destinada principalmente a alumnos de Magisterio, cuya formación didáctica es fundamental; pero también indicado para estudiantes preuniversitarios.

Inicialmente realizan una comparación de las definiciones del concepto de Magnitud y de los ejemplos que la suelen acompañar, en libros de texto de Matemáticas y de Física, y exponen que las diferencias aparecidas, tanto en la definición como en los ejemplos mostrados, llevan a crear conflictos cognitivos en el estudiante.

Para unificar estas definiciones, aparentemente diferentes, proponen el uso matemático de la definición, pues aporta rigurosidad; sin embargo los elementos físicos y sus ejemplos, ayudan a comprender la abstracción que lleva la definición matemática.

A continuación exponen algunas definiciones relacionadas con el concepto de magnitud, por ejemplo, el significado de Propiedad de un elemento y la acompañan de ejemplos diversos; también indican que hay propiedades como el tiempo o la longitud que son primarias, no se definen y los estudiantes las van percibiendo desde los primeros años de manera intuitiva; a partir de ahí, el concepto de Propiedad de un objeto induce una magnitud cuando en el conjunto de los estados de la propiedad se cumplan una serie de propiedades matemáticas.

Finalmente, concluyen que los libros de texto suelen tener definiciones que llevan a errores u obstáculos en la comprensión del concepto, y exponen ejemplos físicos en los que se puede observar el cumplimiento de aquellas propiedades matemáticas: conmutativa, asociativa, elemento neutro, etc.

Los autores hacen un análisis detallado sobre el número de Oro, frecuentemente utilizado como modelo de componente matemática estética, por su presencia habitual en la Naturaleza y en las Artes. Exponen algunas cuestiones, relaciones y construcciones geométricas relacionadas con polígonos regulares y estrellados en los que aparece el número de Oro.

Después de recordar la obtención de la relación áurea por los griegos y de exponer la obtención el valor del número ϕ, a partir de la división áurea de un segmento, detallan también la relación que tiene con su valor inverso, 1/ϕ, de modo que ϕ-1 = 1/ϕ para, a continuación, exponer diversas maneras gráficas de obtener el segmento áureo.

A partir de ese punto realizan un análisis de la presencia del segmento áureo en los pentágonos regulares, que se establece entre el lado del pentágono y una diagonal de éste. Por tanto, se puede construir fácilmente un pentágono regular a partir de su lado, basta para ello con tener previamente su diagonal, después de la obtención del segmento áureo.

Por último, realizan otro estudio minucioso de la presencia de la proporción áurea en el decágono, donde el lado es el segmento áureo del radio de una circunferencia circunscrita; entonces, a partir de esa relación se puede construir también el decágono regular, conocido su lado y obteniendo su segmento áureo previamente.

José Martel y sus colaboradores tratan el clásico problema de la cuadratura del círculo, con sus connotaciones históricas y los diferentes intentos y métodos para resolverlo, con la propuesta de utilización en el aula de Matemáticas.

Los autores comienzan describiendo el clásico problema de la cuadratura del círculo, de difícil solución; es decir, se trata de construir un cuadrado de igual área que la de un círculo dado, utilizando únicamente las herramientas euclidianas, esto es: regla y compás.

Teniendo en cuenta lo anterior, este problema no tiene solución, tal y como demostró Lindemann en 1882; pero en este análisis exponen diversos métodos que se han empleado, a lo largo de la historia, para construir ese cuadrado de forma aproximada. Ya, desde los años 1800 a.C., los egipcios habían resuelto el problema, tomando ocho novenos del diámetro para el lado del cuadrado.

También los griegos en el siglo V a.C., trataron este problema y, en los siglos IV y III a.C., Dinostrato y Arquímedes respectivamente, dieron también una solución aproximada, a partir de la trisectriz de Hipias y de la espiral de Arquímedes; ambos métodos quedan detallados en este artículo.

Posteriormente, aportan dos métodos que dan soluciones aproximadas, usando solo regla y compás y proponen además, que tales métodos pueden ser tema de investigación en el aula con estudiantes de Magisterio, dados su valor didáctico y cultural, pues se hace uso de la Historia al relacionar la enseñanza de los conceptos con los problemas que los crearon y su desarrollo.

El primer método que exponen, se basa en la rectificación de la circunferencia, debida a Kochanski, que resulta un método gráfico y visual de gran sencillez en su realización; esta construcción se muestra a continuación mediante un applet de Geogebra.