La ecuación de segundo grado a través de la historia
Se realiza un amplio recorrido histórico sobre el uso de las ecuaciones de segundo grado y su resolución, algunas veces ingeniosas, en diversas culturas, desde la antigua Babilonia hasta el Renacimiento.
El profesor Martel resalta que, de los descubrimientos hechos de muestras de escritura cuneiformes de la antigua Babilonia y de su interpretación, se deduce que en aquellos tiempos (1800 a 1600 a.C.) ya sabían resolver ecuaciones del tipo x2+q=px, usando la suma y el producto de sus raíces (x1+x2=p, x1x2=q) y la semidiferencia de éstas; con estos datos obtenían un sencillo sistema lineal de dos ecuaciones con dos incógnitas, (x1+x2)/2 = p/2 y (x1-x2)/2 = √((p/2)2-q).
Expone además, en este primer apartado, una serie de ejemplos y curiosidades extraídas de los hallazgos babilónicos. Es necesario resaltar la importancia de estas situaciones mostradas, como ejemplo de uso de la historia de la matemática como recurso en el aula; pues ofrece al estudiante datos para comprender la naturaleza de los conocimientos matemáticos, su razón de ser y su vertiente humana, pues no se trata de un bloque de conocimientos artificial, creado, fijo y terminado; sino que es fruto de la actividad humana y se han desarrollado en algún momento de la historia de la humanidad por necesidad de uso y han evolucionado hasta la actualidad.
Posteriormente hace mención a unos papiros, datados entre 1991 y 1778 a.C., que tratan problemas matemáticos que se solucionan con ecuaciones de segundo grado. A continuación, la antigua China es señalada también con la mención a una recopilación de problemas matemáticos, el Jiuzhang suanshu, que parece que fueron resueltos del mismo modo que en las antiguas civilizaciones babilónicas.
De la época griega, resalta a Diofanto, que en su obra Aritmética, halló la solución general de ecuaciones del tipo ax2±bx=±c. Con Brahmagupta da paso a los hindúes, quienes redujeron los casos de Diofanto a uno solo y explica que fueron éstos quienes comenzaron a dar las raíces por parejas y a admitir raíces negativas como soluciones.
A continuación realiza un análisis extenso del uso de ecuaciones cuadráticas por los árabes, donde cita a Al-Khwarizmi, quien en su Compendio de cálculo por restauración y comparación (Hisab Al-jabr wa’l muqabalah), utiliza métodos puramente geométricos para la resolución de las ecuaciones de segundo grado del tipo ax2±bx=±c.
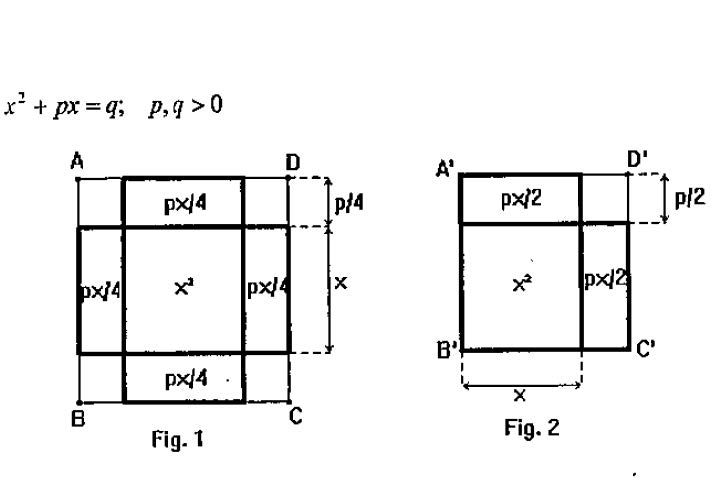Dos modos visuales de para encontrar la solución a x2+px-q=0 a partir de un cuadrado ABCD
Con la referencia a François Viète analiza la sustitución de los métodos geométricos por los analíticos; además expone su manera de resolver ecuaciones de segundo grado mediante una sustitución de variables, método que se sigue empleando en ecuaciones de tercer y cuarto grados.
Como consideraciones finales, José Martel muestra con un ejemplo, que una ecuación general de segundo grado puede ser también fácilmente resuelta por el método de los antiguos babilonios o por el cuadrado geométrico de los árabes, además del método usado en la actualidad, basado en la formación de un cuadrado algebraico.