Relación entre el área de un triángulo y el área del cuadrilátero interior
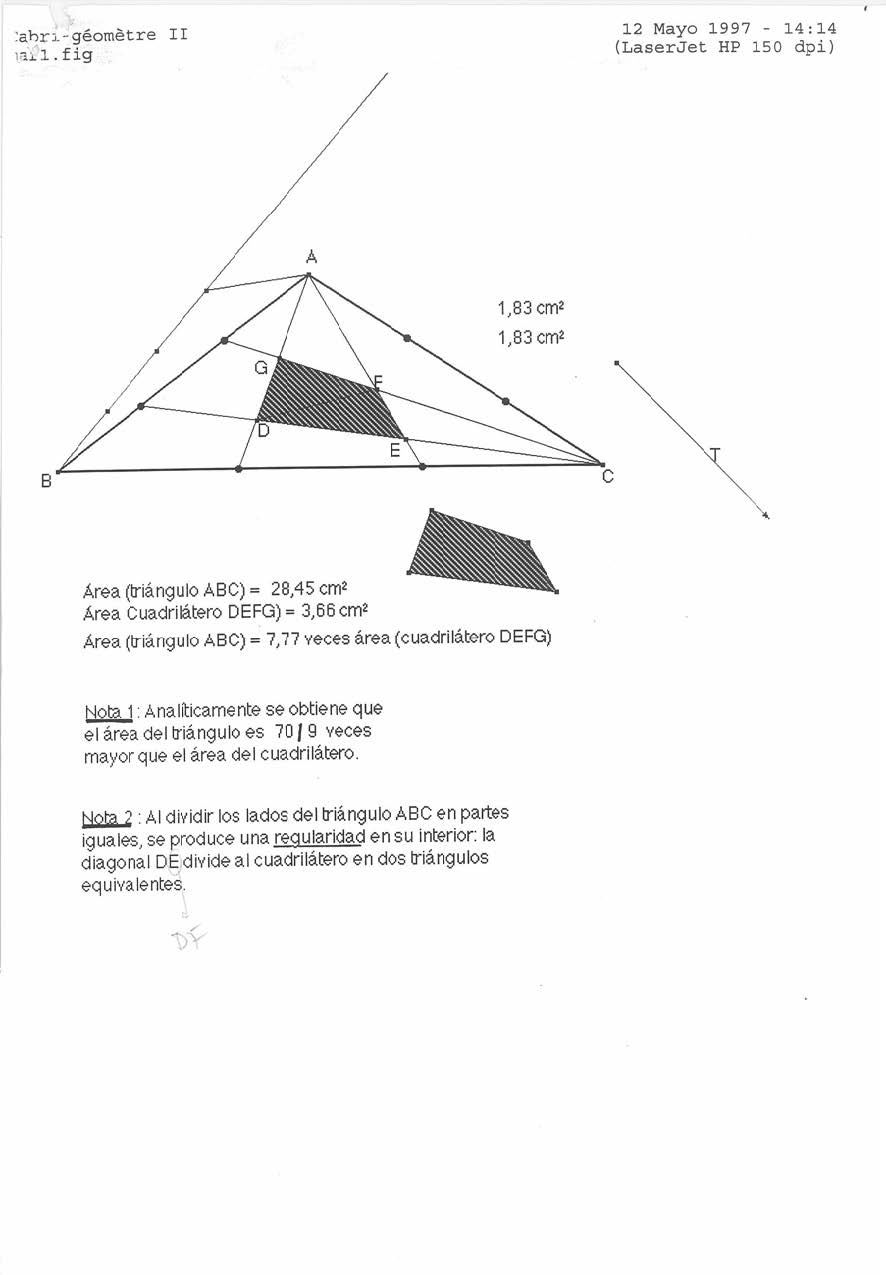
En el año 1997, planteaba la relación existente entre el área de un triángulo cualquiera, ABC y el área del cuadrilátero, DEFG, que se obtiene al trazar rectas desde dos vértices del triángulo hasta puntos situados en los lados opuestos, estando estos divididos en (2n+1) partes iguales. Realiza un caso particular inicial, al dividir los lados del triángulo en tres partes iguales, y analíticamente y con ayuda de Cabri II, obtiene que la relación entre ambas áreas es, k = 70/9; también hace una anotación o curiosidad, la diagonal DF del cuadrilátero, que mira hacia el vértice común a los dos lados divididos, lo parte en dos triángulos equivalentes.
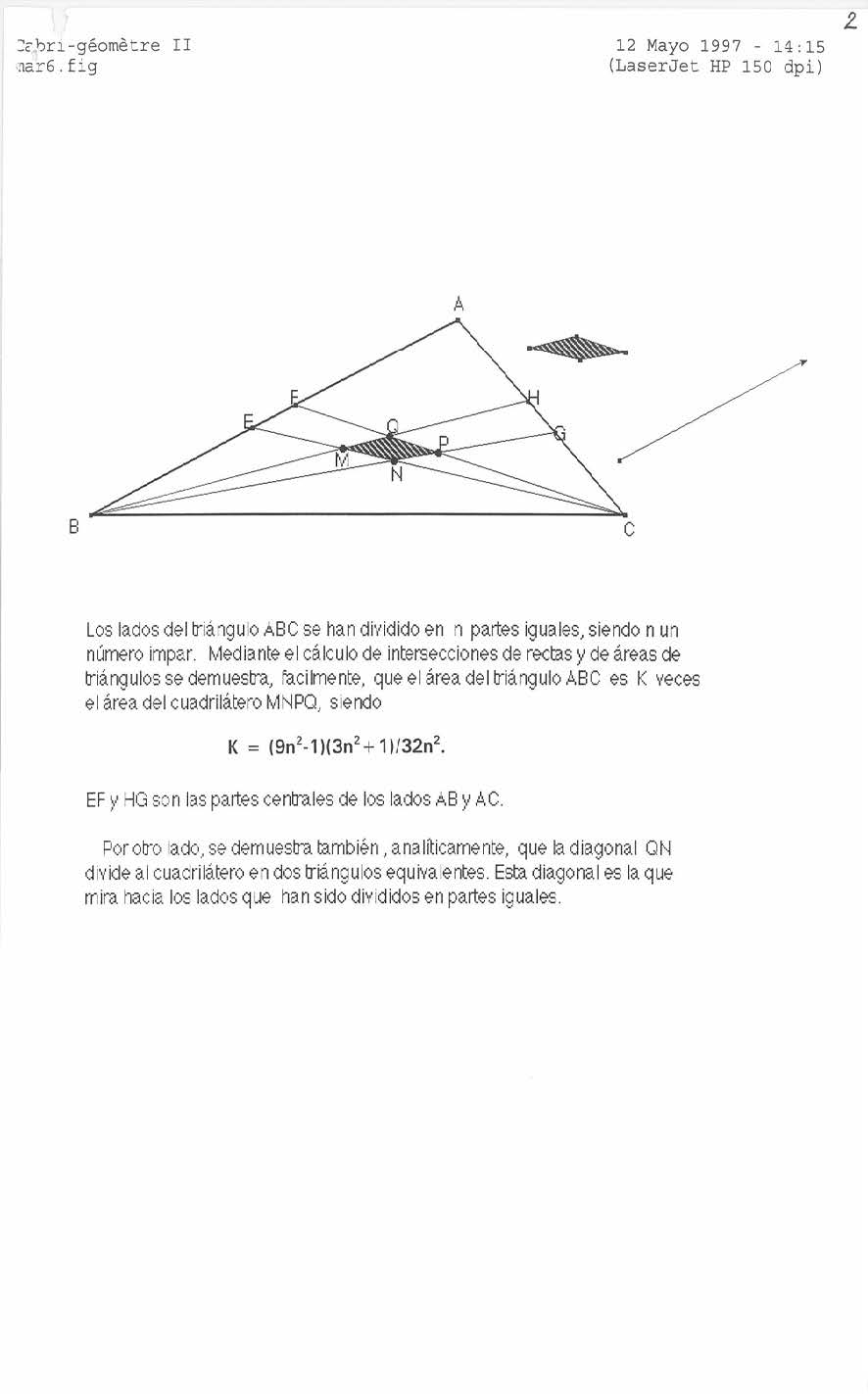
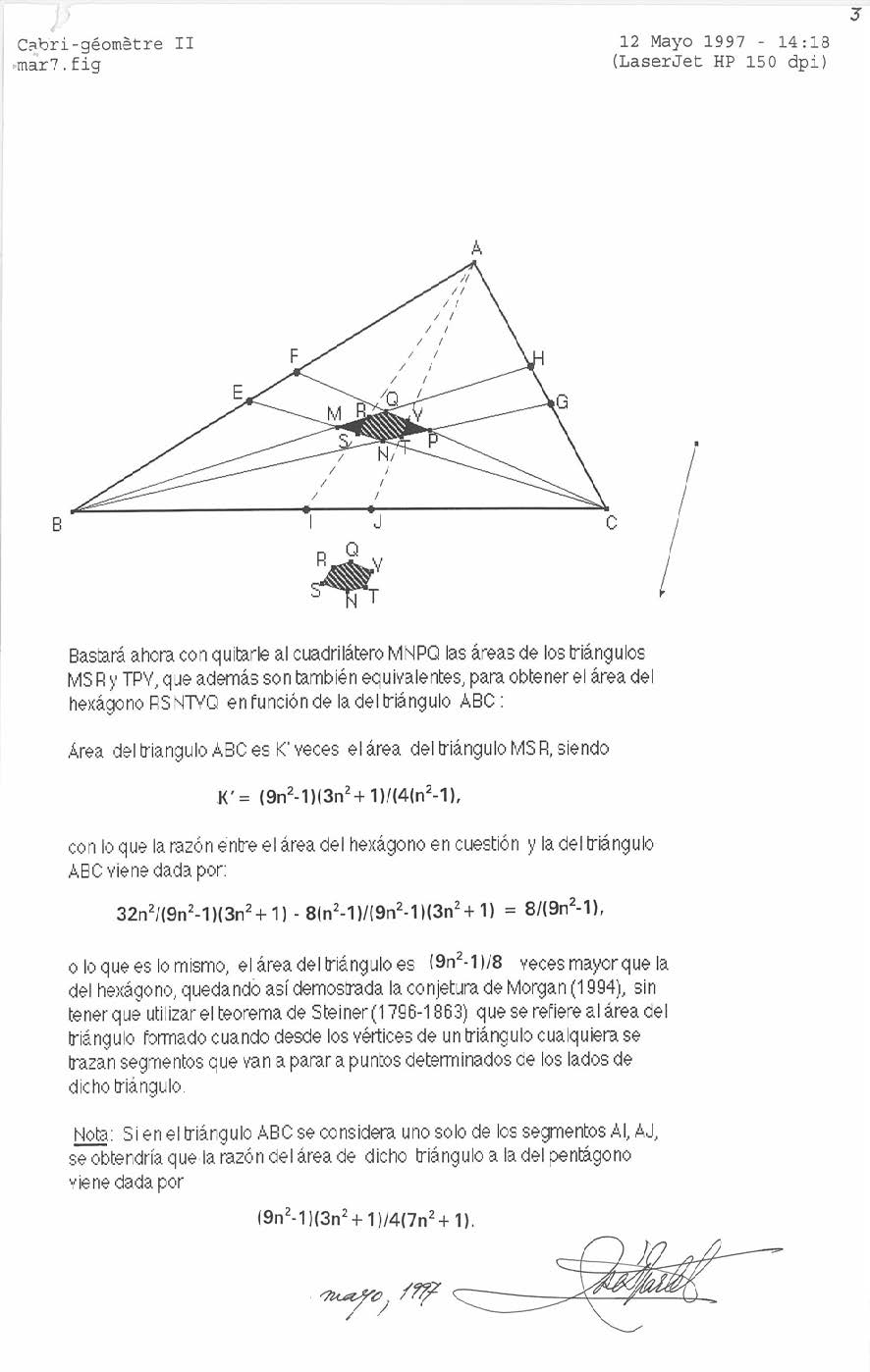
Posteriormente hace una generalización, al dividir dos de los lados en (2n+1) partes iguales, a partir de un cálculo de intersecciones de rectas y de áreas demuestra que la relación k, entre las áreas del triángulo y del cuadrilátero, puede obtenerse de la expresión k = (9n2-1) (3n2+1)/32n2. Si la división se hace para los tres lados del triángulo, lo que se obtiene es un hexágono, en este caso, la relación k’, entre el área del triángulo ABC y el área del hexágono es k = (9n2-1)/8; este análisis realizado por el profesor Martel se añade por completo a continuación.